Options Deep Dive - Learning Vega in a different way
As I'm mostly doing income trades, vega is a huge factor in how I trade. I believe the definition of vega is pretty easily available out there. Just for quick recap of definition:
Vega is the Greek that measures an option’s sensitivity to implied volatility. It is the change in the option’s price for a one-point change in implied volatility.
So, what does that actually means? What I'm gonna do is to simulate few scenarios on risk curve to show what exactly vega is doing to better understand vega. I hope through this few scenarios, I will further enhance my understanding on vega and you will get a much better idea how vega affects your trade. Let's start with setting some background context to the scenario.
Selling a SPY 53 DTE PUT, at different delta.
At the money
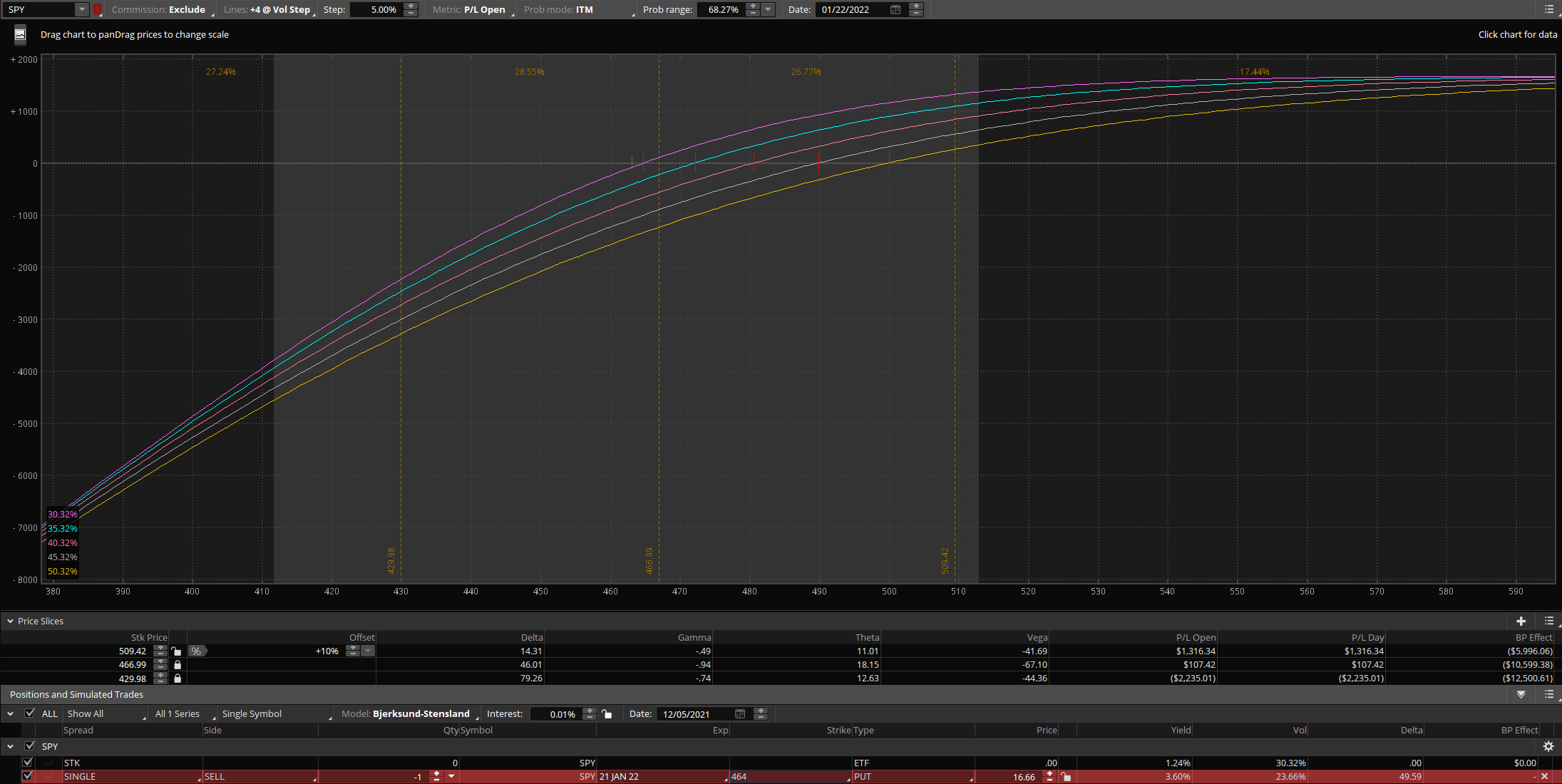
Each lines in this risk curve shows the different volatility steps (+5%). To get a better relativity for later comparison, I'll run through the numbers here.
We are selling a -0.5 delta put at credit of $16.66 ($1666).
When price is near at the money, each step UP of volatility loses about $300-400 in value.
When price is about 1 standard deviation away, each step UP of volatility loses about $200-300 in value.
Keep that in mind, let me flip the curve to volatility steps (-5%) instead.
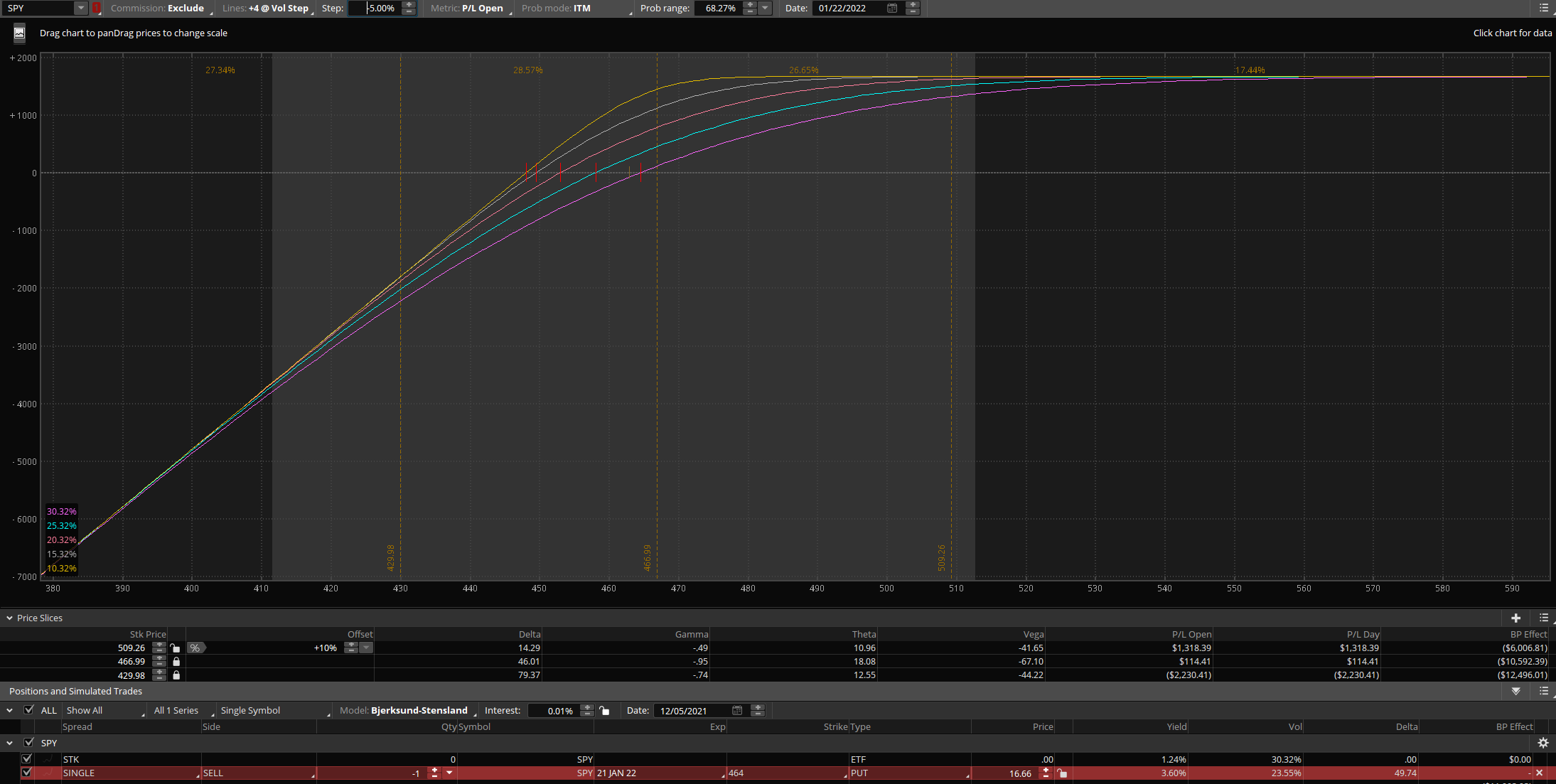
Now when price is near the money, each step DOWN in volatility gains about $300+ in value.
and when price is about 1 standard deviation away both sides, each step DOWN in volatility gains only less than $100 in value.
So what does that tells us?
Selling at or near the money put, gains the most from volatility coming down. And once the stock price moves away from the put strike, the profit gets lesser and lesser.
There's 2 things I take away from this, when selling at the money:
- We definitely want to sell when volatility is high, because when volatility comes down we profit.
- When price moves away from the money, the biggest gains and losses happens in the initial move. As it gets further away from the money, volatility reduces.
This means when price moves up, usually volatility will also drop, we should take profit early as going higher won't make as much as the initial move.
Out of the money
So how different is it when it's out of the money.
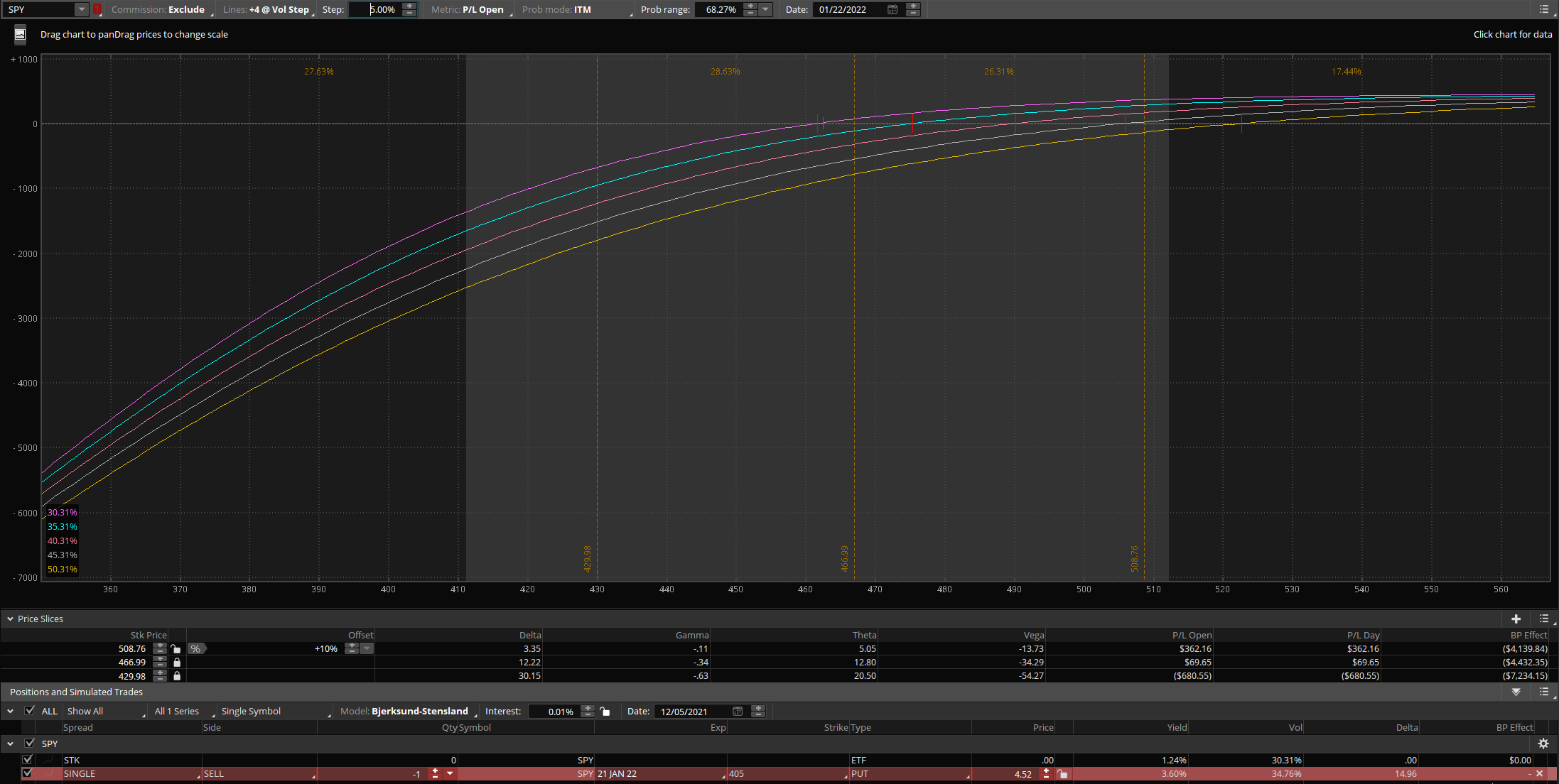
We are selling a -0.15 delta put at credit of $4.52 ($452).
When price is at the money, each step UP of volatility loses about $150-250 in value.
When price is about 1 standard deviation UP, each step up of volatility loses about $100-150 in value.
When price is about 1 standard deviation DOWN, each step up of volatiltiy loses about $300+ in value.
Let's see the volatiltiy step down (-5%).
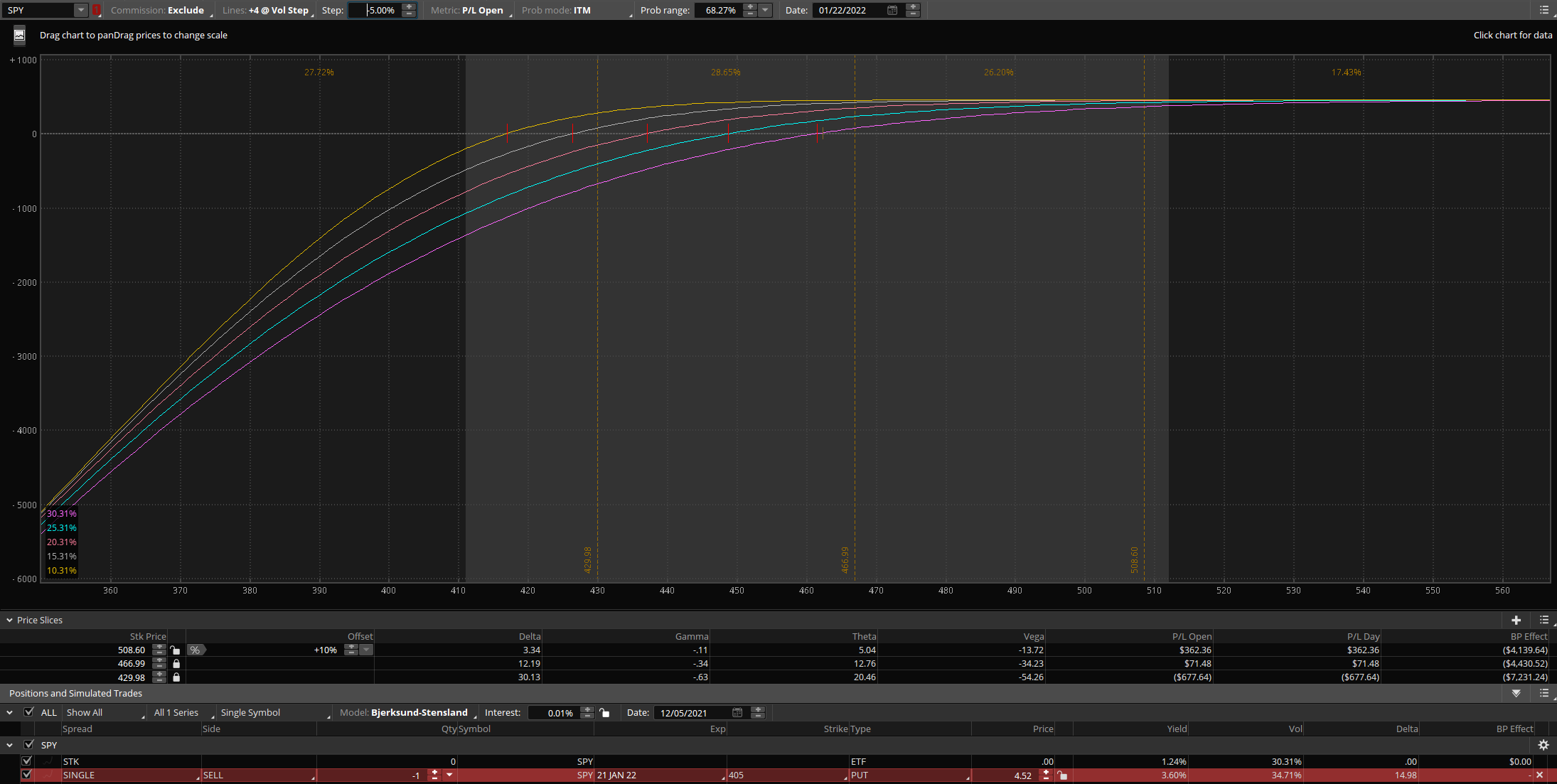
When price is at the money, each step DOWN in volatiltiy gains about $50-150.
When price is about 1 standard deviation UP, each step DOWN in volatility gains less than $40.
When price is about 1 standard deviation DOWN, each step DOWN in volatility gains about $300+.
So what's the take away here when selling out of the money:
- Similarly, we want to sell when volatility is high. So when volatility goes down we profit from it.
- When price goes down, the losses grows with vega. Means if it goes down further, your losses can be exponential.
Conclusion?
The beauty about options is in different scenarios, there are different variables that benefits you. But the important thing is to understand the underlying concepts and in this case, Vega is the important topic here.
I hope the above scenarios gives you a different way to understand vega, at least to me it does. It could be applied to all the different options combo. Just try your strategies out on the risk curve, analyse and see how you can put vega to your favor.
This is just a simple exercise to give a sense of how Vega behave differently, I might go into more complex combo scenarios in future posts. Stay tuned!






Member discussion